AVL trees are self-balancing binary search trees, ensuring efficient data retrieval through a clever balancing mechanism. This guide, packed with interactive elements, will illuminate how these trees work, even if you’re new to computer science. Think of AVL trees as self-organizing bookshelves. They constantly rearrange themselves to stay balanced, ensuring quick access to your “books” (data).
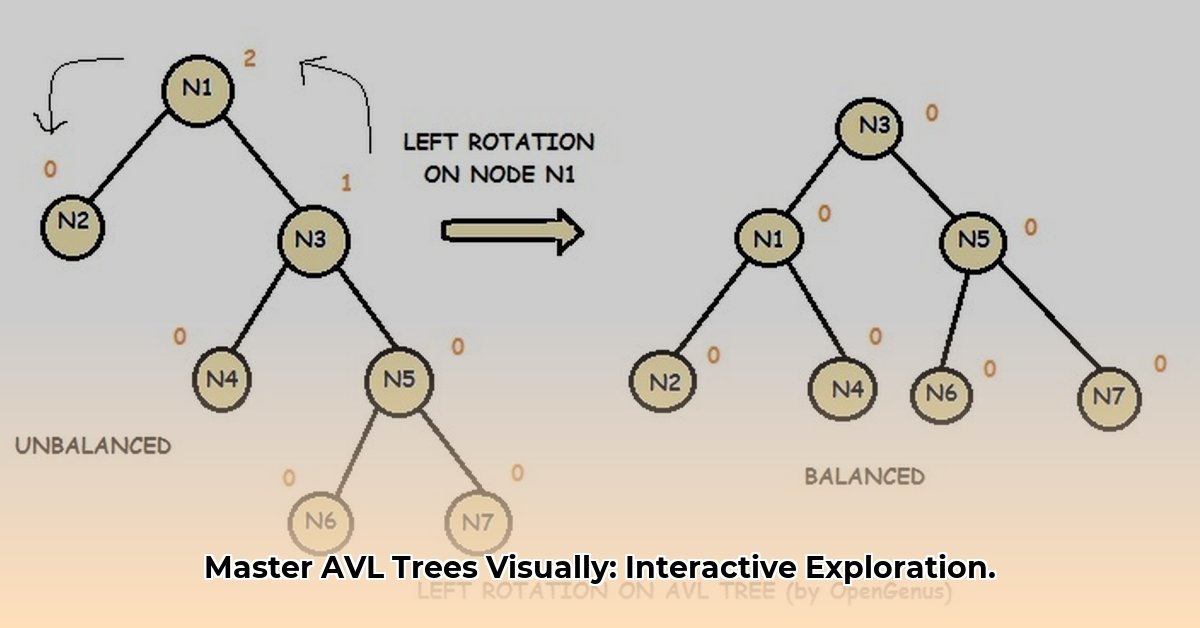
The Balancing Act: Balance Factors and Rotations
The key to this self-organization is the balance factor. Each node (a data point) in the tree has a balance factor, representing the height difference between its left and right subtrees. This factor can only be -1, 0, or 1. If it goes beyond this range, the tree performs a “rotation” to restore balance. These rotations are the secret sauce of AVL trees, like a little dance the tree performs to stay upright.
Understanding Balance Factors
Imagine a seesaw. If one side is much heavier, it tilts. The balance factor acts like a tiny level on each node, indicating the “tilt.” A balance factor of 0 means perfect balance, -1 suggests a slight left lean, and 1 a slight right lean. If the “tilt” gets too extreme (-2 or 2), a rotation is triggered.
Rotations: The Tree’s Rebalancing Dance
There are four main types of rotations:
LL (Left-Left): Corrects a left-heavy lean.
RR (Right-Right): Corrects a right-heavy lean.
LR (Left-Right): Corrects a combined left-then-right lean.
RL (Right-Left): Corrects a combined right-then-left lean.
These rotations are best understood visually. Explore interactive AVL tree visualizations that animate these rotations, transforming complex algorithms into intuitive displays.
Hands-on with AVL Tree Operations
Let’s explore how insertion, deletion, and search work in AVL trees, using the analogy of our self-balancing bookshelf.
Insertion: Adding a New Book
Find the Right Spot: Just like placing a book on a shelf, you find the correct position for the new node based on its value.
Check the Balance: After placing the “book,” the bookshelf checks its balance at each level upwards.
Rotate (If Necessary): If any “shelf” is unbalanced, the bookshelf performs the required rotations to regain stability.
Deletion: Removing a Book
Remove the Book: Take the “book” off the shelf.
Check the Balance: Just like with insertion, the bookshelf checks its balance upwards.
Rotate (If Necessary): Perform rotations to restore balance if needed.
Searching: Finding a Specific Book
Searching is straightforward. You start at the top “shelf” and follow the tree’s structure, comparing the value you seek with each node’s value. The balanced nature of the AVL tree ensures a quick search, even with many “books.”
Interactive Exploration: Bringing AVL Trees to Life
Interactive AVL tree visualizers offer a powerful way to grasp these concepts. Experiment with these actions:
Insertion: Add nodes and watch the rotations unfold.
Deletion: Remove nodes and observe the rebalancing act.
Search: Follow the search path and appreciate the efficiency of a balanced tree.
Try building an AVL tree with the numbers 3, 2, 1, 4, 5, 6, and 7. Observe the rotations and balance factor changes. This hands-on experience solidifies understanding.
Choosing an Interactive Visualizer
Different visualizers offer varying features:
Feature
Ideal Visualizer
Interaction
High
Rotations
Animated
Balance Factor
Displayed
Code Examples
Included (optional)
Look for a visualizer with high interactivity, animated rotations, and clear display of balance factors. Code examples can be a bonus.
Beyond the Basics: Further Exploration
AVL trees are a starting point. Explore other self-balancing trees like red-black trees and B-trees, each with strengths and weaknesses suited for specific applications. Ongoing research continues to refine these data structures, making it a dynamic field of study. While our current understanding is robust, future research may yield even more efficient balancing algorithms.
AVL Trees vs. Red-Black Trees: A Quick Comparison
Feature
AVL Tree
Red-Black Tree
Balance Condition
Stricter (balance factor -1, 0, or 1)
More relaxed
Rotations
More frequent
Less frequent
Search
Potentially slightly faster
Potentially slightly slower
Insertion/Deletion
Potentially slightly slower
Potentially slightly faster
The best choice depends on your application’s specific needs. AVL trees might be preferable for search-intensive tasks, while red-black trees might be more suitable for frequent insertions and deletions.
This interactive guide, combined with visual exploration, provides a robust understanding of AVL trees and their role in efficient data management. Remember, this dynamic field is constantly evolving, with ongoing research potentially leading to new insights and optimizations. This suggests that staying updated with the latest advancements is crucial for anyone working with these data structures.
I am a writer who loves renewable energy, with a focus on sustainable living, renewable energy, and eco-friendly innovation. With a passion for environmental awareness and a desire to explore the latest trends in green technology, corporate sustainability, and climate action. Through in-depth storytelling
